Entrevista al catedrático Luis María Abia Llera

*¿SE PUEDE COMPUTAR TODO?*

1 ¿ Que le animó a estudiar su carrera y cuales fueron sus mayores puntos de apoyo para continuar mejorando?

2 ¿ Le gustaría haberse dedicado a la investigación o a la docencia?

3 ¿ Como cree que deberían ser impartidas las matemáticas, es decir , el mejor método para el aprendizaje?

4 ¿ Le parece mejor lugar para exponer sus conocimientos una universidad o a gente de niveles inferiores como puede ser un instituto?

5 ¿ Después de haber estudiado matemáticas, ve el mundo de la misma manera que antes?

6 ¿Cómo deberían  entenderse las matemáticas en estos momentos?

7 ¿Si pudiera computar cualquier cosa, qué sería y por qué?

 8 ¿Hay algún enigma matemático que le gustaría llegar a resolver? 

Conceptos y coordenadas de un vector libre

Los vectores de un sistema libre son linealmente independientes por lo tanto estos sistemas también se puedes llamar de vectores linealmente independientes ( los vectores de los sistemas ligados serán vectores linealmente dependientes)



Bases

Coordenadas de un vector libre

Comienza la geometría analítica cuando hablamos de coordenadas.

Vector: una pareja de números

Vector ortogonal y sistemas de vectores

Vector ortogonal

Este tipo de vectores también se llaman perpendiculares pero la forma rigurosa de nombrarlos es ortogonales 

(utilizamos el plural ya que si u es ortogonal a v, entonces, v es ortogonal a u ).

Sistema de vectores

Los diferentes conjuntos creados pertenecerán al mismo subconjunto ya que los sistemas son diferentes por las siguientes propiedades :

1. Los vectores se pueden repetir
2. El orden en el que se coloquen los vectores si importa

Rectas

 Posición relativa de dos rectas en el plano (según sus puntos) 

Ejercicios números complejos

a)      1-i                                                            b)    3+3i

 

c)       -5 + 7i                                                     d)    5 – 9i

 

e)     6 + i                                                          f)     3 + i  

 

a) -14 + 8i                               b)  -14/25  +   23/25 i

c) -3 -4i                                   d) -4/5  - 3/5i

 
e)  10                                       f) 4/5 – 7/5 i

a)    (3 – 4i) ∙ (3 – 4i)= -7 -24i

 

b)   (1-i) ³ = -2 -2i

 

c)    3 - i

 

d)   -77 + 207i

Ejercicios geometría vectorial

EJ 1 

EJ 2

Siempre que tengamos 2 vectores NO nulos con distinta dirección cualquier vector se puede expresar como combinación lineal y de forma única.

EJ 3

Operaciones con vectores

Operación: proceso por el cuál se emparejan dos o más elementos del mismo conjunto para dar otro de ese mismo conjunto

 Suma y resta

Propiedades de la suma:

- Operación bien definida: el resultado es único.

- Conmutativa u + v = v + u

- Asociativa

- Elemento neutro: es el vector nulo 0 o el AA

Producto por escalar

(un escalar en un número real)

Vector unitario

Combinación lineal de vectores

Geometría analítica en el plano, Vectores

 La geometría del plano puede ser: clásica o euclidiana, vectorial y analítica 


VECTORES

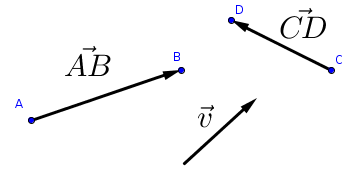
Un vector fijo es un segmento orientado entre dos puntos llamados origen y extremo.
Los vectores se representan con letras minúsculas con una flechita encima o mediante dos letras mayúsculas que representan los puntos origen y extremo.

Elementos de un vector

 Módulo: es la longitud del vector, es decir, la distancia del origen al extremo. Se expresa entre barras verticales: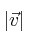 
 Dirección: la recta que contiene al vector (o cualquier otra paralela)
 Sentido: es la orientación del vector (la flecha que dibujamos en su extremo indica su orientación)

 Si tenemos un vector cuyos puntos son iguales y no tiene ni dirección ni sentido lo llamamos vector nulo (su módulo es 0)

Vectores equipolentes

Dos o más vectores son equipolentes cuando tienen el mismo módulo, misma dirección y mismo sentido.

Propiedades de la relación de equipolencia:

- Reflexiva: todo vector fijo está relacionado consigo mismo.

- Simétrica: si un vector fijo es equipolente a otro, este otro es equipolente al primero. Podemos decir que son equipolentes (utilizamos el plural porque es una relación simétrica).

- Transitiva: si un vector fijo es equipolente a otro y éste lo es a un tercero, el primero es equipolente al tercero.

Cuando una relación binaria tiene estas 3 propiedades la llamamos relación de equivalencia.

Llamamos relación binaria a la relación R existente entre dos elementos a y b, de dos conjuntos A y B respectivamente. Indicando que el elemento a está relacionado con b.

Clase de equivalencia: conjunto de todos los vectores equipolentes con AB.

Vector libre: clase de equivalencia de un vector fijo. 

El conjunto de todos los vectores libres del plano se llama V 2

Ecuaciones con complejos

Ecuaciones con complejos

Siempre es posible encontrar las soluciones o raíces tanto reales como complejas de una ecuación (dentro del conjunto de los complejos).

El número de soluciones se corresponde con el grado de la ecuación.

Producto, cociente, potenciación y radicación de números complejos en forma polar

Producto

 z = |z|_a y w = |w|_b 
 entonces:

Cociente

  z = |z|_a y w = |w|_b 

entonces: 

Potencia 

  ,

 entonces:                                                  

Fórmula de Moivre

 

Forma trigonométrica:  z = |z|·(cos a + i sen a).

 . 

Forma trigonométrica:  |z|ⁿ·(cos na + i sen na) y ( |z|·(cos a + i sen a))ⁿ. Si igualamos las dos expresiones y módulos=1 obtenemos la fórmula de MOIVRE:

(cos a + i sen a)ⁿ = cos na + i sen na

Radicación

 , 

entonces: 

si w es una raíz n-ésima de z, entonces wⁿ = z.

 Si  y , entonces:  

(El 2kp aparece porque el argumento de un número complejo no es único, sino que, como ya hemos visto, todo número complejo tiene infinitos argumentos.)

Por tanto 

Forma polar y trigonométrica de un complejo

Módulo y argumento de un complejo

El módulo de un número complejo z = (a,b) es la distancia del origen de coordenadas al afijo de dicho número.

El módulo de z es , y se representa por |z|.

El argumento de un número complejo  es el ángulo que forma el semieje positivo real con el segmento que une el origen de coordenadas y el afijo del número ( medido en sentido contrario a las agujas del reloj) Se representa por arg(z) = a  y se calcula tg a=b/a

Un número complejo tiene infinitos argumentos, si a es un argumento de un número complejo z, entonces también lo es a + 2kp.  
Se llama argumento principal de un número complejo al único argumento de éste que está en el intervalo ]0,2p)

Forma polar

Un número complejo z del que conocemos su módulo |z| y su argumento a lo podemos escribir como |z|a, a esta forma se le llama forma módulo-argumental o polar.

Forma trigonométrica

Se llama forma trigonométrica a |z|·(cos a + i sen a):

Potencia de un número complejo

La potencia (a + bi)n  de un número a + bi con exponente natural se hace desarrollando la potencia del binomio (a + bi)

OJO: hay que tener en cuenta los valores que toman las sucesivas potencias del número i

Suma, resta y división de complejos

  Operación: aplicación de una pareja de números de un determinado conjunto (producto cartesiano) en la que su manipulación da lugar a un resultado en el mismo conjunto.

 La suma de números complejos se realiza sumando partes reales entre sí y partes imaginarias entre sí.

( a + bi) + (c + di) = (a + c) + (b + d)i

Ej

( 5 + 2 i) + ( −8 + 3 i) = (5 − 8) + (2 + 3)i = −3 + 5i

Resta de números complejos

La diferencia de números complejos se realiza restando partes reales entre sí y partes imaginarias entre sí.

(a + bi) − (c + di) = (a − c) + (b − d)i

( 5 + 2 i) + ( − 8 + 3 i) − (4 − 2i ) = (5 − 8 − 4) + (2 + 3 + 2)i = −7 + 7i

División de números complejos 

Para dividir números complejos en forma binómica se multiplica numerador y denominador por el conjugado del denominador y se realizan las operaciones correspondientes.

Multiplicación e inverso de un número complejo

Multiplicación e inverso de un número complejo

Números complejos

Números complejos

Definición:

 Ecuación con solución en C:

 Representación de números complejos en la gráfica: