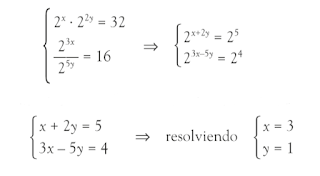Algunos ejercicios del examen

Resolución de problemas

Los pasos a seguir serían

1. Lee y comprende el enunciado del problema tantas veces como sea necesario.
2. Identifica la incógnita o incógnitas.
3. Plantea la ecuación/inecuación/ecuaciones/inecuaciones identificando la información relevante.
4. Resuelve la ecuación/inecuación o los sistemas de ecuaciones/inecuaciones.
5. Responde a lo que te preguntan valorando la solución adecuada del contexto.

Inecuaciones de primer grado con 2 incógnitas y sus sistemas

Inecuaciones de primer grado con 2 incógnitas

Sistemas de inecuaciones de primer grado con 2 incógnitas

Inecuaciones racionales

Inecuaciones racionales

Son del tipo

Examen grupal primer trimestre

El examen fue realizado en grupos previamente formados por nuestro profesor y ahora os traigo dos de los ejercicios que aparecían en él.

Ej 11:

Definición de polinomio

Un polinomio es una expresión algebraica de forma :

que se forma por la unión de dos o más variables vinculadas a través de operaciones de multiplicación resta o suma.

Un requisito indispensable que debe cumplir para llamarse polinomio es :

y constan de lo siguiente:

Ej 37:

¿Qué edad tenía mi hijo en el año 2002 sabiendo que dicha edad era igual a la suma de las cifras del año en que nació?

Teniendo en cuenta el enunciado planteamos lo siguiente

Inecuaciones de segundo grado

Sistemas de inecuaciones

Sistemas de inecuaciones

Inecuaciones

Una vez claro este termino será aplicado en las siguientes entradas

Ecuaciones logarítmicas

Para la resolución de este tipo de ecuaciones nos encontramos con dos casos:

y

Logaritmos y ecuaciones logarítmicas

Logaritmos

Propiedades de los logaritmos






Ecuaciones logarítmicas

Ecuaciones y sistemas de ecuaciones exponenciales

Ecuaciones exponenciales 

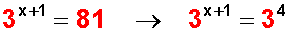
Una ecuación es exponencial cuando la incógnita aparece en el exponente de una potencia

Tenemos dos formas de resolver estas ecuaciones

1 Reducir a potencias de igual base

Si los dos miembros de la igualdad tienen distinta base, debemos reducirlos a la misma base.

igualaríamos los exponentes y "despejaríamos la x"

2  Recurrir a un cambio de variable.

                                               

OJO: deshacemos el cambio de variable

Sistemas de ecuaciones exponenciales

Un sistema de ecuaciones es exponencial si al menos una de sus ecuaciones lo es

Se resolverían de las mismas dos formas que las ecuaciones

1 Reducir a base común 

2 Cambio de variable 

Reflexión

Cómo ser un estudiante exitoso: las cualidades que debes tener

Existen ciertas cosas que una persona puede hacer para convertirse en un buen estudiante. Sin embargo, para lograrlo, debe poseer ciertas características. Estas son innatas para muchos, pero quienes no las tienen pueden desarrollarlas. Así como alguien puede hacer cosas para convertirse en un buen estudiante, también puede desarrollar las características necesarias para ser un estudiante exitoso.

Más tarde te explica estas características.

http://www.ehowenespanol.com/estudiante-exitoso-cualidades-debes-como_156414/

En mi opinión esto no es cierto ya que no todo el mundo puede realizar esta tarea de aprender (o simplemente en determinadas materias) ya que veo necesarias unas cualidades con las que naces y que no se pueden desarrollar así como las ganas de aprender y de mejorar.
Por eso creo que cuando se va avanzando en la vida la gente se especializa en determinadas materias porque no todo el mundo tiene la capacidad de realizar las mismas acciones (ni todos pueden ser ingenieros ni todos pueden ser mecanicos por mucho que lo trabajes e intentes).

El taller de nuestras vidas

/https://dametresminutos.wordpress.com/2015/08/26/el-taller-de-nuestras-vidas/

No tienes que fijarte en tus puntos débiles y para lo que no sirves por mucho que te esfuerces sino que, te tienes que centrar en tus puntos fuertes y en lo valioso que eres en muchos otros aspectos de la vida y aun más si le añadimos el trabajo en equipo ya que tus puntos débiles quedarían equilibrados con los de los demás y tu equilibrarías lo suyos.

Ni somos perfectos ni somos iguales pero eso nos hace unirnos con la intención de mejorar.

Repaso tema 2

 1 TEOREMA DEL RESTO

El resto de la división de un polinomio P(x), entre un polinomio de la forma (x − a) es el valor numérico de dicho polinomio para el valor: x = a.

TEOREMA DEL FACTOR 

A un polinomio P(x) es divisible por el monomio de la forma (x - a) ,si (x = a) = 0.

Al valor x = a se le llama raíz de P(x).

Las raíces de un polinomio son los valores que anulan el polinomio.

2 FACTORIZAR UN POLINOMIO

Igualamos el polinomio a 0 para encontrar sus raíces

y estas serán sus factores o divisores.

(Habría mas formas explicadas en entradas anteriores)



3 FRACCIONES ALGEBRAICAS 

Una fracción algebraica es el cociente de dos polinomios y se representa por:

Dos fracciones algebraicas son equivalentes:

si se cumple que P(x) · S(x) = Q(x) · R(x).

Simplificación de fracciones algebraicas

Para simplificar una fracción algebraica se divide el numerador y el denominador de la fracción por un polinomio que sea factor común de ambos.

4 OPERACIONES CON               FRACCIONES ALGEBRAICAS

Suma y diferencia de fracciones algebraicas

Fracciones algebraicas con igual denominador

La suma de fracciones algebraicas con el mismo denominador es otra fracción algebraica con el mismo denominador y cuyo numerador es la suma de los numeradores.

Producto de fracciones algebraicas

El producto de dos fracciones algebraicas es otra fracción algebraica donde el numerador es el producto de los numeradores y el denominador es el producto de los denominadores.

Cociente de fracciones algebraicas

El cociente de dos fracciones algebraicas es otra fracción algebraica con numerador el producto del numerador de la primera por el denominador de la segunda, y con denominador el producto del denominador de la primera por el numerador de la segunda.

5 DESCOMPOSICIÓN DE FRACCIONES ALGEBRAICAS EN SUMAS DE FRACCIONES SIMPLES

*Los demás puntos estarían explicados en entradas anteriores 

12 MÉTODO DE GAUSS

El método de Gauss consiste en transformar un sistema de ecuaciones en otro equivalente de forma que este sea escalonado

Para facilitar el cálculo vamos a transformar el sistema en una matriz, en la que pondremos los coeficientes de las variables y los términos independientes (separados por una recta).

 

Transformaciones elementales

Sistemas de ecuaciones equivalentes

Son aquellos que tienen las mismas soluciones

• Si aplicamos a un sistema las transformaciones elementales obtendremos sistemas equivalentes

Transformaciones elementales sobre un sistema de ecuaciones 

Ecuaciones: irracionales, de grado mayor que 2, sistemas

La resolución de ecuaciones de grado mayor que dos

 Por el momento solo la podemos realizar de dos formas o con dos tipos de ecuaciones 

Ecuaciones irracionales

Fórmulas de Cardano

Cardano fue un matemático del que previamente hemos reflexionado en una entrada anterior.

Desarrolló una serie de fórmulas para las ecuaciones de segundo grado mediante las cuales sabiendo las raíces del  polinomio se puede determinar este polinomio .

Ecuaciones de primer y segundo grado

Ecuaciones equivalentes

Repaso de las propiedades de las operaciones

Propiedades de las operaciones 

Propiedades de las operaciones básicas

Las operaciones básicas son la suma, la resta, la multiplicación, la división y la potencia.

Propiedades de la suma

Propiedad conmutativa: La propiedad conmutativa indica que al cambiar el orden de dos sumandos, no altera el resultado, por ejemplo si sumamos 5 + 3 el resultado será 8, y al revertir las cifras; 3 + 5 seguirá dando 8

Propiedad asociativa: Esta propiedad es parecida a la conmutativa, la diferencia es que esta señala que cuando se suman tres o más números independientemente como estén ordenados el resultado es el mismo. Ejemplo: 7 + 5+ 9 es 21, al igual que 9 + 7 + 5.

Propiedad distributiva: La propiedad distributiva dice que la suma de dos números multiplicada por un tercero, va a dar igual resultado que multiplicar cada uno de esos números individualmente por el mismo tercero y luego sumarlos. Ejemplo: 3 (4 + 2) = 18, al igual que (3 x 4) + (3 x 2) = 18.

Elemento neutro: Trata de que, al sumar cualquier número con el cero, va dar de resultado el número original, un ejemplo: 4 + 0 = 4.

Propiedades de la resta

Propiedad no conmutativa: Al contrario de la suma, a la resta si le es cambiada el orden de sus cifras cambia su resultado, porque el orden que tienen las cifras influye mucho en el total. Ejemplo: 3 – 1 = 2, pero 1 – 3= -3, es decir, en ocasiones el resultado suele pasar a ser un número negativo, cambiando drásticamente el total.

Propiedad no asociativa: De esta propiedad al igual que la conmutativa también carece la resta, ya que es muy parecida a la anterior, por lo tanto sucede lo mismo, el resultado cambiará si alteran el orden de las cifras.

Propiedad modulativa: También llamada elemento neutro, esta, dice que al restar cualquier número por el cero, va a dar de resultado el número original. Ejemplo: 3 – 0 = 3.

Propiedad Distributiva: Esta propiedad implica que, al multiplicar por un número cualquiera el resultado de una resta, el resultado va a dar igual, a multiplicar cada uno de los números a restar individualmente y luego restarlos, ejemplo: 2 (4 - 3) = 2 es igual a (2 x 4) – (2 x 3)  = 2.

Propiedades de la multiplicación

Propiedad conmutativa: Esta propiedad dice que; el orden de los factores no altera al producto, es decir, 2 x 3= 6, al igual que 3 x 2= 6, el resultado es el mismo, aunque los factores estén ordenados de distinta forma.

Propiedad asociativa: Esta propiedad se aplica cuando, multiplicas 3 o más números y le cambias el orden de los factores, al hacer esto no cambiará el resultado y será el mismo. Ejemplo: 4 x 7 x 3 = 84  y al cambiar el orden de los factores; 3 x 7 x 4 = 84 también.

Propiedad de elemento neutro: La propiedad de elemento neutro indica que, al multiplicar cualquier número por el uno, va a dar de resultado el número inicial, por ejemplo: 5 x 1 = 5.

Propiedad distributiva: Esta, es igual a la de la suma, porque, por ejemplo, al multiplicar: 9 (7 + 6) va a dar igual resultado que al multiplicar: (9 x 7) + (9 x 6).

Propiedad del cero: La propiedad del cero, es muy simple, ya que lo dice es que; todo número multiplicado por cero es igual a cero mismo, sea cual sea el número va a dar cero, ejemplo: 791289334637028 x 0 = 0

Propiedades de la división

Propiedad distributiva: Dividir la suma de dos números, es igual que dividir cada una de esas cifras por separado y luego sumarlas, ejemplo: (12 + 18) ÷ 6 es igual a (12 ÷ 6) + (18 ÷ 6), en ambas es igual a cinco.

Propiedad del cero: Esta propiedad dice que el cero dividido entre cualquier número da siempre 0. Esto tiene mucho sentido, porque por ejemplo, si no tenemos ningún pastelillo que repartir, a todos nos tocará 0 pastelillos. Dando un ejemplo numérico; 0 ÷ 8 = 0

Estas propiedades son las únicas que tiene la división, sin embargo tiene varias no propiedades, ya que, no es conmutativa, ni asociativa.

Propiedades de la potencia

Propiedad de exponente cero: Esta dice, que un número (que no sea cero) elevado a 0 siempre va a dar 1, sea cual sea la base si esta elevada a 0 va a dar de resultado 1, ejemplo: 176901642109⁰ = 1

Propiedad de exponente uno: Se trata de que cualquier potencia que tenga de exponente el número 1 siempre va a dar de resultado la misma base, sea cual sea, ejemplo: 58¹= 58.

Potencia de exponente negativo: Esta funciona cuando un número elevado a un exponente negativo, es igual al inverso de la misma expresión pero, pasa a ser positivo, ejemplo: 3^-2 = 3^0-2, más fácil expresarlo de esta forma: 3⁰/3^-2  = 1/3^-2.

Multiplicación de potencias de igual base: Al multiplicar potencias de igual base se conserva la base y se suman sus exponentes, por ejemplo: 3² x 3⁶ = 3⁸, después de esto se resuelve la potencia normalmente.

División de potencias de igual base: En la división de potencias de igual base se conserva la base y se restan los exponentes, por ejemplo: 9⁵ x 9² = 9³, y después de esto al igual que en la multiplicación se resuelve la potencia de forma normal.

Propiedad distributiva: Esta funciona de igual forma que las demás operaciones tratadas, ejemplo: (4 x 5)² es igual a: 4² x 5²

Ecuaciones polinómicas

Concepto: 
Una ecuación es una igualdad matemática entre dos expresiones algebraicas, denominadas miembros, en las que aparecen valores conocidos , y desconocidos o incógnitas, relacionados mediante operaciones matemáticas.

Sophie Germain

Marie-Sophie Germain (1 de abril de 1776 - 27 de junio de 1831) fue una matemática francesa que hizo importantes contribuciones a la teoría de números y la teoría de la elasticidad. Uno de los más importantes fue el estudio de los que posteriormente fueron nombrados como números primos de Sophie Germain (números primos cuyo doble incrementado en una unidad es también un número primo). Matemática, física y filósofa. A pesar de la oposición de sus padres y las dificultades presentadas por una sociedad sexista. Debido al prejuicio contra su sexo, no pudo establecer una carrera en matemáticas, por lo que trabajó independientemente a lo largo de su vida. Fue autodidacta, disfrazándose de hombre para poder entrar a estudiar en lugares de matemáticos (donde solo dejaban entrar varones). En sus investigaciones y estudios, los autografiaba como "Sr. Leblanc", para ocultar su identidad, de este modo durante años pudo avanzar sus conocimientos y exponer y presentar ideas nuevas.

Ella consiguió seguir adelante y vencer o engañar a una        

sociedad machista que le impedía hacer lo que mas deseaba y gracias que lo hizo porque sus aportaciones fueron muy relevantes y significativas. Fue un pequeño paso para la igualdad de géneros ,la cual no existía en esa época, demostrando que las capacidades de un hombre son idénticas a las de una mujer.

Aportaciones matemáticas

-Identidad de Sophie Germain :

- Teoría de Números. Demostraba que si x, y, z son números

enteros, tales que x5+y5+z5=0 entonces, al menos uno de 

los números x, y o z debe ser divisible por 5

-El Teorema de Germain constituyó un paso importante para demostrar el último teorema de Fermat. De hecho a partir de entonces la demostración se dividió en dos casos: el primero consistía en probarlo cuando ninguno de los números x, y, z es divisible por n, y el segundo cuando uno sólo de los tres números es divisible por n. Además con esta clasificación el primer caso del Teorema de Fermat para n =5 quedaba probado. (En 1825 Legendre y Dirichlet completaron la demostración para n = 5 en el segundo caso.)

-El teorema de Sophie Germain demuestra que si n es un número primo tal que 2n +1 es primo, entonces el primer caso del teorema de Fermat es verdadero. El trabajo se había simplificado a lamitad. En Teoría de Números se dice que un número natural es un número primo de Germain, si el número n es primo y 2n+1 también lo es. Los números primos de Sophie Germain inferiores a 200, son: 2, 3, 5, 11, 23, 29, 41, 53, 83, 89, 113, 131, 173, 179, 191.

- Investigaciones en teoría de la 
elasticidad